Contents
Ejercicio 2: Hallar el vector X para la siguiente ecuacion matricial
A=[4 -2 -10; 2 10 -12; -4 -6 16];
B=[-10; 32; -16];
X=A\B
X =
2.0000
4.0000
1.0000
Ejercicio 4: Hallar los autovalores y autovectores de la matriz A
A=[0 1 -1; -6 -11 6;-6 -11 5];
[X,D]=eig(A)
T1=A*X
T2=X*D
X =
0.7071 -0.2182 -0.0921
0.0000 -0.4364 -0.5523
0.7071 -0.8729 -0.8285
D =
-1.0000 0 0
0 -2.0000 0
0 0 -3.0000
T1 =
-0.7071 0.4364 0.2762
-0.0000 0.8729 1.6570
-0.7071 1.7457 2.4856
T2 =
-0.7071 0.4364 0.2762
-0.0000 0.8729 1.6570
-0.7071 1.7457 2.4856
Ejercicio 5: determinar los voltajes de los nodos V1 y V2 y la potencia entregada por cada fuente
Y=[1.5-2i -0.35+1.2i ;-0.35+1.2i 0.9-1.6i];
I=[30+40i; 20+15i];
disp('Solucion: ')
V=Y\I
S=V.*conj(I)
Solucion:
V =
3.5902 +35.0928i
6.0155 +36.2212i
S =
1.0e+03 *
1.5114 + 0.9092i
0.6636 + 0.6342i
Ejercicio 6: Escribir una funcion recursiva para resolver le problema de las torres de Hanoi y probarla para 5 discos
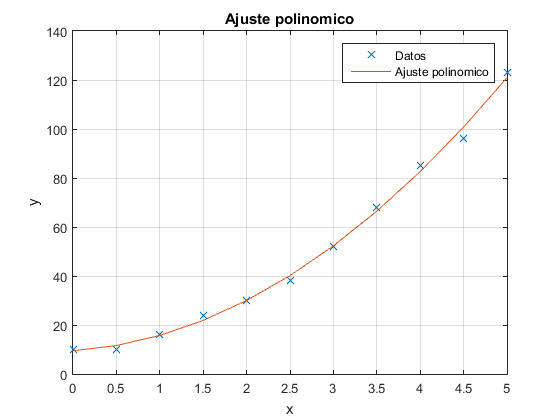
Ejercicio 7: Ajustar el polinomio de orden 2 y graficar los resultados
x=[0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5];
y=[10 10 16 24 30 38 52 68 85 96 123];
p=polyfit(x,y,2)
yc=polyval(p,x)
plot(x,y,'x',x,yc)
xlabel('x'),ylabel('y'),grid,title('Ajuste polinomico')
legend('Datos','Ajuste polinomico',4)
p =
4.0093 2.2443 9.4895
yc =
Columns 1 through 7
9.4895 11.6140 15.7431 21.8769 30.0154 40.1585 52.3063
Columns 8 through 11
66.4587 82.6159 100.7776 120.9441
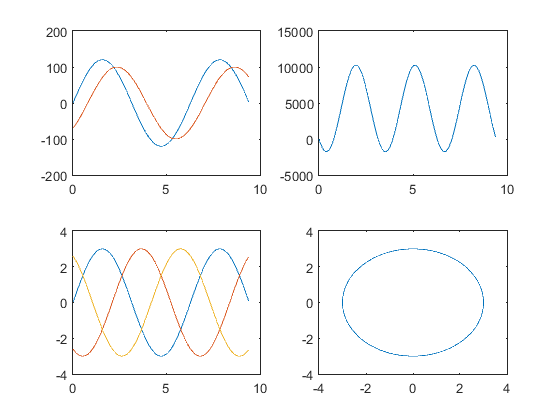
Ejercicio 8: Graficar las funciones
x=[0:0.05:3*pi];
subplot(2,2,1);
plot(x,120*sin(x));
hold on;
plot(x, 100*sin(x-pi*.25));
subplot(2,2,2);
plot(x,120*sin(x)*100.*sin(x-(pi*.25)));
subplot(2,2,3);
plot(x,3*sin(x));
hold on;
plot(x,3*sin(x-2*(pi/3)));
hold on;
plot(x,3*sin(x-4*(pi/3)));
subplot(2,2,4);
ang=0:0.01:2*pi;
xp=3*cos(ang);
yp=3*sin(ang);
plot(xp,yp);
Ejercicio 11 : Hallar las raices del polinomio
p=[1 0 -35 50 24];
a=roots(p)
a =
-6.4910
4.8706
2.0000
-0.3796
Ejercicio 12: Resolver la ec diferencial
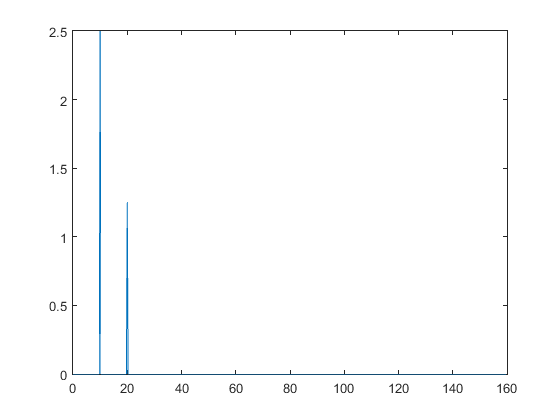
Ejercicio 13: Graficar las señales
k = 5; m = 10; fo = 10; Bo = 2.5;
N = 2^m; T = 2^k/fo;
ts = (0:N-1)*T/N;
df = (0:N/2-1)/T;
g1 = Bo*sin(2*pi*fo*ts)+Bo/2*sin(2*pi*fo*2*ts);
An1 = abs(fft(g1, N))/N;
figure
plot(df, 2*An1(1:N/2))
g2 = exp(-2*ts)+sin(2*pi*fo*ts);
An2 = abs(fft(g2, N))/N;
figure
plot(df, 2*An2(1:N/2))
g3 = sin(2*pi*fo*ts)+5*sin(2*pi*(fo/10)*ts);
An3 = abs(fft(g3, N))/N;
figure
plot(df, 2*An3(1:N/2))
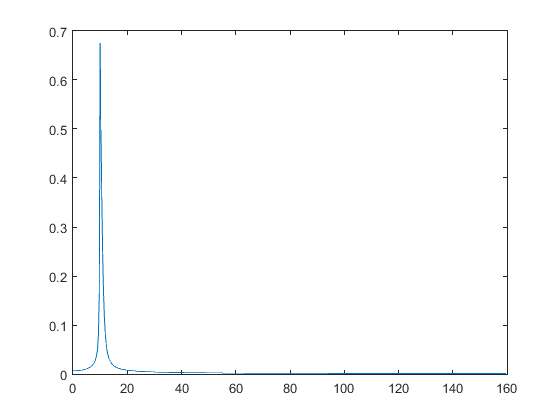
g4 = sin(2*pi*fo*ts-5*exp(-2*ts));
An4 = abs(fft(g4, N))/N;
figure
plot(df, 2*An4(1:N/2))


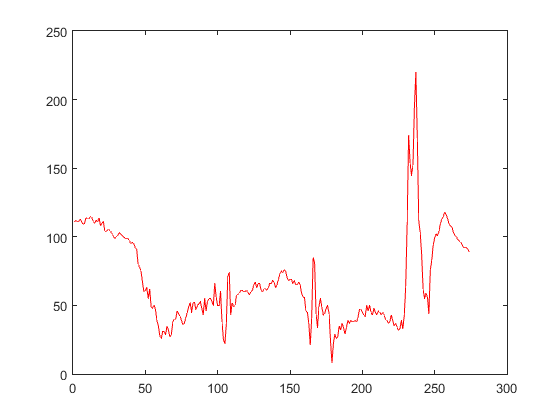
Ejercicio 14: Leer y graficar la imagen
v = imread('WindTunnel.jpg');
image(v)
axis image off
figure
row=200;
red = v(row, :, 1);
plot(red, 'r');
hold on